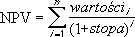NPV

Oblicza wartość bieżącą netto inwestycji dzięki zastosowaniu stawki rabatu i serii przyszłych płatności (wartości ujemne) oraz przychodów (wartości dodatnie).

Składnia

NPV(stawka,wartość1,wartość2, ...)

Stawka jest stawką rabatu w danym okresie.

Wartość1, wartość2, ... są argumentami (od 1 do 29) oznaczającymi płatności i przychody.

Wartość1, wartość2, ... musi być równomiernie rozmieszczona w czasie i występować na końcu każdego okresu.
Funkcja NPV wykorzystuje kolejność wartość1, wartość2, ... w celu zinterpretowania kolejności wpływów gotówkowych. Należy pamiętać, aby wprowadzać wartości płatności i przychodów w odpowiedniej kolejności.
Uwzględniane są argumenty, które są liczbami, wartościami logicznymi, odwzorowaniami tekstowymi liczb lub są puste; argumenty, które są wartościami błędów lub tekstem, którego nie można przełożyć na liczby, są ignorowane.

Spostrzeżenia

Inwestycja NPV rozpoczyna się jeden okres przed datą wpływu gotówkowego wartość1 i kończy wraz z ostatnim wpływem gotówkowym z listy. Obliczenia NPV są oparte na przyszłych wpływach gotówkowych. Jeżeli pierwszy wpływ gotówkowy następuje na początku pierwszego okresu, pierwsza wartość musi zostać dodana do wyniku NPV, a nie do wartości argumentów. Aby uzyskać więcej informacji, zobacz poniższe przykłady.
Jeżeli n jest liczbą przepływów gotówkowych z listy wartości, formuła funkcji NPV jest następująca:
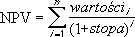
Funkcja NPV jest podobna do funkcji PV (wartość bieżąca). Podstawową różnicą między funkcjami PV i NPV jest to, że funkcja PV umożliwia rozpoczęcie przepływów gotówkowych na końcu lub na początku okresu. W przeciwieństwie do zmiennych wartości przepływów gotówkowych NPV przepływy gotówkowe PV muszą być stałe w całym okresie trwania inwestycji. Aby uzyskać informacje dotyczące rent i funkcji finansowych, zapoznaj się z danymi dotyczącymi funkcji PV.
Funkcja NPV jest także związana z funkcją IRR (wewnętrzna stopa zwrotu). IRR jest stawką, dla której NPV równa się zero: NPV(IRR(...), ...) = 0.

Przykład 1

W poniższym przykładzie:

Stawka jest roczną stawką rabatu.
Wartość1 to pierwotny koszt inwestycji za rok od dziś.
Wartość2 to zwrot z pierwszego roku.
Wartość3 to zwrot z drugiego roku.
Wartość4 to zwrot z trzeciego roku.

Stawka	Wartość1	Wartość2	Wartość3	Wartość4	Formuła	Opis (Wynik)
10%	-10000	3000	4200	6800	=NPV([Stawka], [Wartość1], [Wartość2], [Wartość3], [Wartość4])	Wartość bieżąca netto inwestycji (1188,44)

W poprzednim przykładzie uwzględniono koszt wstępny 10 000 PLN jako jedną z wartości, ponieważ płatność występuje na końcu pierwszego okresu.

Przykład 2

W poniższym przykładzie:

Stawka jest roczną stawką rabatu. Może to być stopa inflacji lub stopa odsetek konkurencyjnej inwestycji.
Wartość1 to pierwotny koszt inwestycji za jeden rok od dziś.
Wartość2 to zwrot z pierwszego roku.
Wartość3 to zwrot z drugiego roku.
Wartość4 to zwrot z trzeciego roku.
Wartość5 to zwrot z czwartego roku.
Wartość6 to zwrot z piątego roku.

Stawka	Wartość1	Wartość2	Wartość3	Wartość4	Wartość5	Wartość6	Formuła	Opis (Wynik)
8%	40000	8000	9200	10000	12000	14500	=NPV(Stawka, [Wartość2], [Wartość3], [Wartość4], [Wartość5], [Wartość6])+[Wartość1]	Wartość bieżąca netto inwestycji (1922,06)
8%	40000	8000	9200	10000	12000	14500	=NPV(Stawka, [Wartość2], [Wartość3], [Wartość4], [Wartość5], [Wartość6], -9000)+[Wartość1]	Wartość bieżąca netto inwestycji ze stratą w szóstym roku 9000 (-3749,47)

W poprzednim przykładzie nie uwzględniono kosztu wstępnego 40 000 PLN jako jednej z wartości, ponieważ płatność występuje na początku pierwszego okresu.