Sygnały okresowe – to takie, które w dziedzinie czasu można opisać funkcją x(t) taką, że istnieje T należące do przedziału 0<T<+¥, że dla każdej chwili czasu t zachodzi równość: 

x(t+T) = x(t),

przy czym wartość T nazywa się okresem sygnału.

Sygnały nieokresowe – sygnały, dla których nie jest spełniony warunek okresowości.

Sygnały harmoniczne – to takie, które w dziedzinie czasu można opisać funkcją harmoniczną:

x(t) = A × cos (2×p×f_o×t + j)

            gdzie:

                        A – amplituda sygnału (np. w mm),
                        f_o – częstotliwość (w Hz, czyli liczbie cykli na sekundę),
                        2×p×f_o = w_o – częstotliwość kątowa (w rad/s),
                        j - przesunięcie fazowe (rad),
                        t – rozpatrywana chwila czasu (s).

Sygnały poliharmoniczne – to takie, które są kombinacją liniową co najmniej dwóch sygnałów harmonicznych, zwanych sygnałami składowymi. Liczba składowych sygnału poliharmonicznego może być w ogólnym przypadku nieskończona. Poniżej przedstawiono przykład opisu matematycznego sygnału poliharmonicznego złożonego z sumy dwóch składowych harmonicznych:

x(t) = A₁ × cos (2×p×f_o1×t + j₁) + A₂ × sin (2×p×f_o2×t + j₂)

Aby sygnał mógł być uznany za poliharmoniczny, częstotliwość każdej jego składowej musi być całkowitą wielokrotnością pewnej częstotliwości f zwanej częstotliwością podstawową.

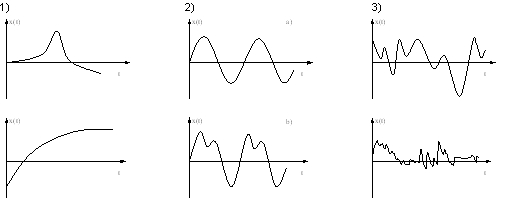
Rys.2. Przykłady realizacji sygnałów: 1) nieokresowych, 2) okresowych: a) harmonicznego,
           b) poliharmonicznego, 3) losowych.

<<poprzednia strona  |  następna strona >>