2.5. SYGNAŁY HARMONICZNE

Na Rys. 3. przedstawiono przykładowy przebieg sinusoidalnego sygnału harmonicznego, przy czym: A – reprezentuje amplitudę przebiegu, a j - jest przesunięciem fazowym mierzonym w [rad] od początku osi czasu. Rozpatrywany sygnał jest okresowy, a więc powtarza się co jeden pełny okres (cykl). Liczba okresów sygnału w jednostce czasu, zliczona w czasie 1 sekundy realizacji sygnału, nosi nazwę częstotliwości sygnału f_o i wyrażana jest w Hz. Zależność pomiędzy okresem sygnału a częstotliwością jest następująca:

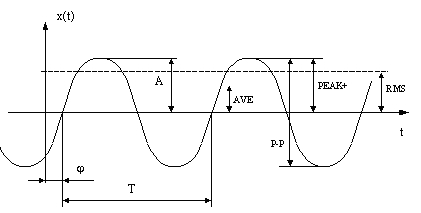
Rys.3. Przykładowy przebieg sygnału harmonicznego (funkcja sinusoidalna)

Sygnały harmoniczne opisywane są również za pomocą cech liczbowych. Są to:

Wartość średnia (AVE):

Wartość skuteczna (RMS):  - jest to pierwiastek z wartości średniej podniesionej do kwadratu

 

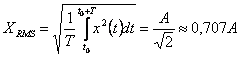
Wartość szczytowa dodatnia i ujemna (PEAK+, PEAK-):

Wartość międzyszczytowa (szczyt-szczyt; P-P):

Pomiędzy przedstawionymi powyżej wielkościami zachodzą związki, które przedstawiono poniżej w postaci współczynników. Należy również podkreślić, że podane we wzorach wartości liczbowe dotyczą sygnałów harmonicznych.

Współczynnik kształtu (K):

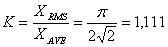
Współczynnik szczytu(C):

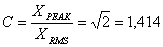
Współczynnik impulsowości (I):

LITERATURA: 

1. K.G.Beauchamp: Przetwarzanie sygnałów metodami analogowymi i cyfrowymi. WNT Warszawa 1978.

2. Cholewa W, Moczulski W.: Diagnostyka techniczna maszyn. Pomiary i analiza sygnałów. Skrypt    uczelniany Politechniki Śląskiej nr1758. Gliwice 1993r.

3. Cholewa W., Kaźmierczak J.: Diagnostyka techniczna maszyn. Przetwarzanie cech sygnałów. Skryptuczelniany Politechniki Śląskiej nr 1693. Gliwice 1992r.

4. Żółtowski B., Ćwik Z.: Leksykon diagnostyki technicznej. Wydawnictwa uczelniane ATR Bydgoszcz. Warszawa 1996

<<poprzednia strona  | przejdź do TESTU SPRAWDZAJĄCEGO